These calculators are used to calculate linear motion. If you need to calculate limited angle rotary motion, please use the rotary motion calculators.
Newton's Second law:
$$ F = m \times a $$
Force = Mass x Acceleration
To size a stage properly the force must be known. If force is not known it must be calculated from this equation. The mass is the total mass of the customer payload plus the mass of the moving components of the stage. If the acceleration component is not known it must be calculated. Calculators are provided under the Acceleration tab for estimating the acceleration of a system. Once the force is determined, the duty cycle for all of the specific forces must be determined to calculate the RMS force, which is the average required force. The Force RMS tab provides the tools needed to determine the RMS Force of a motion profile.
- Triangular Acceleration
- Trapezoidal Acceleration
- Sinusoidal Acceleration
- Force RMS
- Duty Cycle
- Force At Duty Cycle
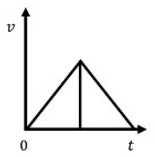
$$ \Large \alpha = \frac{4 \times d }{t^2 \times G} $$
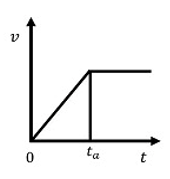
$$\Large a = {2 \times d \over t_{a}^2 \times G} $$
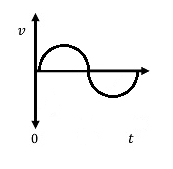
$$ \Large a = {2 \pi^2f^2 D \over G} $$

$$ \Large F_{rms} = \sqrt{\left ( F_{a} \right )^2 \times t_{a} + \left ( F_{c} \right )^2 \times t_{c} + \left ( F_{d} \right )^2 \times t_{d} \over \left ( t_{on} + t_{off} \right )} $$
$$ \Large Duty Cycle\left ( \% \right ) ={ t_{on} \over \left ( t_{on} + t_{off}\right )} \times 100 $$
| Example |
|---|
| Duty Cycle = 1 sec on, 3 sec off Duty Cycle = 1/(1+3) = 1/4 Duty Cycle = 25% |
$$ \Large F@100\% = Force At DutyCycle \div \sqrt{ 1 \over DutyCycle} $$
|
Force at 10% Duty Cycle = 1 lb X (1/10%)1/2 Force at 10% Duty Cycle = 1 lb X 3.16 Force at 10% Duty Cycle = 3.16 lbs |
|
Use the following formula for AC motors:
